Tuesday, September 21, 2010
Monday, September 6, 2010
REMEDIAL SESSION
Wednesday, September 1, 2010
Summary for 30/08/10
If a question asked you about drawing the Line Of Symmetry, it means cutting the graph into two exactly similar parts facing each other like a mirror image.
Example:
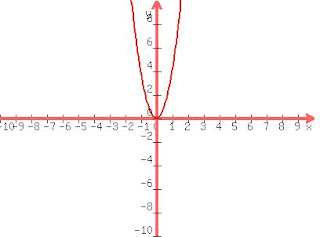
Thursday, August 26, 2010
summary for 22/8/10
- NEVER cross multiply when there is no equal sign in the equation.
- Always do the inner most bracket first.
- All x intercept are called Roots.
- The y intercept of the curve line/parabola is the product of the y intercepts of the original straight lines.
- The x intercept of the curve is the same as the original straight lines.
Wednesday, August 25, 2010
Summary for 24/8/10
Friday, August 20, 2010
Summary for 20/8/10's lesson...
Linear Graphs
For questions similar to example 07 you must REMEMBER that the final line MUST be a equation nothing else.
Also, y=mx+c. In order to find C we need to know y.Therefore,there will only have 1 unknown.
We can substitute some of the coordinates and we can find out what is C.
Finding the Gradient:
We need to change the equation into y=mx+c.
When the questions say it is parallel that means the gradient is the same.
Also,if the line is horizontal the gradient will be 0.
Monday, August 16, 2010
SUMMARY OF LINEAR EQUATIONS ...
- Today we reconsidered the linear equation & the general form of a linear equation is y = mx + c
- where by the m refers to the GRADIENT
- where c is the Y-INTERCEPT (or the value of y when x = 0)
- m is POSITIVE when as x increases, y also increases
- m is NEGATIVE when as x increases, y will decrease
- m is ZERO when as x changes, y is constant (HORIZONTAL LINE)
- m is undefined when x is constant and y changes (VERTICAL LINE)
- X-INTERCEPT would be equal to -c / m ... (or the value of x when y = 0)
Saturday, August 14, 2010
Question 2,
Activity 3 elearning (ong bing jue)
Quadrilaterals have four sides,four angles and the interior angles of each sides added together make up 360 degrees
2a.Quadrilaterals have four sides,four angles and the interior angles of each sides added together make up 360 degrees.A square and a parallelogram both have four sides and angles and these angles make up 360 degrees when added together.Thus a square and parallelogram are quadrilaterals.
2b.Yes.Angles of the opposite sides added together should make 180 degrees which shows they are parallel and never cuts each other.
2c.A trapezoid has only one sides of parallel lines because it has only 2 pairs of opposite angles makes 180 degrees when added together while figures with 4 pairs of opposite angles which makes up 180 degrees when added together has 2 pairs of parallel lines.
Thus All of the above are correct.
3.Only a trapezium which is a quadrilateral has only one parallel lines.
4.No.They make up a rectangle.A parallelogram is made up of a square and 2 triangles.
Let's give an example:(Image Above)
A parallelogram which has a base of 8 cm and height of 3 cm.Let's cut the parallelogram into 3 parts.A rectangle,and 2 triangles,let's combine the 2 triangles and make a square.When you combine the rectangle and the combined rectangle of the two triangles you from a new rectangle of 8 x 3cm. 8 x 3cm is 24 cm square which is not a square number.
5.Since ABCD is a parallelogram and E and F is the midpoints. Since AD = BC and AE=ED which means (AE=ED) is equals to BF =FC thus AE = ED = BF = ED. As angle EBF = AEB
So angle BED + EBF =180 degrees and EDF = EBF.Thus it is a parallelogram.
Friday, August 13, 2010
Maths Activity 3 (Qn 3, 4 and 5)
Q3.
The figure is a trapezoid as it satisfy all the requirement.
Q4.
not all parallelograms are squares as squares have four right angles everytime but parallelogram does not have four right angles all the time.
Q5.
BF and ED is the same as E and F is the midpoint, also, BC and AD are of the same length. when BF and ED are equal, BE and Fd must also be equal as they are now parallel to each other.
Done By JingHeng
(pls ignore the same post below as there is no name)
MAths Activity 3 (Qn 3, 4, 5)
Q3.
The figure is a trapezoid as it satisfy all the requirement.
Q4.
not all parallelograms are squares as squares have four right angles everytime but parallelogram does not have four right angles all the time.
Q5.
BF and ED is the same as E and F is the midpoint, also, BC and AD are of the same length. when BF and ED are equal, BE and Fd must also be equal as they are now parallel to each other.
Math activity 3 (Q1,Q3 and Q4)
Question 3:
Maths e-Learning Activity 3 =>
A conversation between a mentor and a student.
Mentor: Does anyone recall or know what we call it when 2 lines run side-by-side and never cross?
Student: Yes. Lines like that are called parallel lines.
Mentor: Great! We've already learned that quadrilaterals have how many sides?
Student: Four.
Mentor: That's right and we call quadrilaterals with parallel sides parallelograms.
Student: But, how can all the sides be parallel if a quadrilateral is a polygon and is all closed off?
Mentor: Great thinking! I guess what I should have said is that a parallelogram has two pairs of opposite sides that are parallel, like this:
Student: So a rhombus is a type of parallelogram just like a banana is a type of fruit.
Mentor: Right, we should not say that all parallelograms are rhombus, just like we don't say that all fruits are bananas.
Which of the given statements is correct? Justify your answer/s with examples.
A ) A square and a parallelogram are quadrilaterals.
B ) Opposite sides of a square and a parallelogram are parallel.
C ) A trapezoid has one pair of parallel sides.
D ) All the above
Ans:
All of the above
Question 3:
A quadrilateral is drawn on a piece of paper. It has one pair of opposite sides equal in length, the other pair not equal in length, and a pair of opposite angles that are supplementary1. Identify this figure, and justify your answer with reasons.
Ans:
'All parallelograms are squares?' Do you agree with this statement?
Justify your answer with example/s.
Ans:Yes, all four sides of the squares areparallelogram
Question 5:
ABCD is a parallelogram. If E is midpoint of AD and F is midpoint of BC show, with reasons, that BFDE must be a parallelogram.
Question 2,3 and 4 by Ethan Soh
Maths Activity 3. Ng Kok Yin. Question: 1,3,4.
Question 2,3 and 4 By Soe Yan Naung@Norman
Question 2:
Which of the given statements is correct? Justify your answer/s with examples.
A ) A square and a parallelogram are quadrilaterals.
B ) Opposite sides of a square and a parallelogram are parallel.
C ) A trapezoid has one pair of parallel sides.
D ) All the above
Ans: (D). A square and parallelogram both have four sides so they both are quadrilaterals. Both the square and parallelogram has four sides and the opposite sides are parallel to each other which is their property. A trapezoid is a quadrilateral with only two sides parallel to each other like a trapezium.
| Question 3: A quadrilateral is drawn on a piece of paper. It has one pair of opposite sides equal in length, the other pair not equal in length, and a pair of opposite angles that are supplementary1. Identify this figure, and justify your answer with reasons. |
This quadrilateral can be a trapezium which only has one pair of parallel line and two of its sides are of the same length while two are of different lengths. The angles lying on different parallel lines of a side of a trapezium also adds up to 1800.
| Question 4: 'All parallelograms are squares?' Do you agree with this statement? Justify your answer with example/s. |
I do not agree with this statement. A square must have four equal sides but a parallelogram does not need all its sides to be of equal length and a square must have interior angles of 900 only where a parallelogram does not need to be. So, all parallelograms are not squares.
Math E-Learning (Eunice)
Read through the conversation between a mentor and a student.
Mentor: Does anyone recall or know what we call it when 2 lines run side-by-side and never cross?
Student: Yes. Lines like that are called parallel lines.
Mentor: Great! We've already learned that quadrilaterals have how many sides?
Student: Four.
Mentor: That's right and we call quadrilaterals with parallel sides parallelograms.
Student: But, how can all the sides be parallel if a quadrilateral is a polygon and is all closed off?
Mentor: Great thinking! I guess what I should have said is that a parallelogram has two pairs of opposite sides that are parallel, like this:
Mentor: Good. Now I want to tell you about a special kind of parallelogram. It's called a rhombus. A rhombus is a parallelogram, but all four sides have the same length.
Student: So a rhombus is a type of parallelogram just like a banana is a type of fruit.
Mentor: Right, we should not say that all parallelograms are rhombi, just like we don't say that all fruits are bananas.
Question for discussion
Based on the above conversation discuss, with examples and justification whether the following statement is justified.
Answer: This statement is true, as the definition of a rhombus is that opposite sides are parallel to each other, and a square fulfills this definition. However, a square must not only have its opposite sides parallel to each other, the corners must be at a right angle, which means that the not all rhombuses can be a square.
Question 2:
Which of the given statements is correct? Justify your answer/s with examples.
A ) A square and a parallelogram are quadrilaterals.
B ) Opposite sides of a square and a parallelogram are parallel.
C ) A trapezoid has one pair of parallel sides.
D ) All the above
Question 3:
A quadrilateral is drawn on a piece of paper. It has one pair of opposite sides equal in length, the other pair not equal in length, and a pair of opposite angles that are supplementary1. Identify this figure, and justify your answer with reasons.
Answer: This quadrilateral is a trapezium, as definition of a trapezium has at least one set of parallel lines, without stating whether the length of the lines have to be equal, or if the other two lines are parallel to each other or must be of a certain length.
**1 sum of two angles equals 1800
Question 4:
'All parallelograms are squares?' Do you agree with this statement? Justify your answer with example/s.
Answer: No, not all parallelograms are squares. Square must have its corners at a right angle, but not all parallelograms fulfill this condition.
Question 5:
ABCD is a parallelogram. If E is midpoint of AD and F is midpoint of BC show, with reasons, that BFDE must be a parallelogram.
Answer: BF has the same length as ED, and they are parallel to each other, which means that BE and FD are also of the same length and are parallel to each other. When both sets of lines are parallel and have the same length as each other, it will be called a parallelogram.
Question 2,3,4 by Celine Chee
Question 2,4 & 5 by Yeo Jun Peng
Which of the given statements is correct? Justify your answer/s with examples.
A ) A square and a parallelogram are quadrilaterals.
B ) Opposite sides of a square and a parallelogram are parallel.
C ) A trapezoid has one pair of parallel sides.
D ) All the above
Ans : D
Explanation:
Quadrilaterals are a four-sided figure. Both the square and the parallelogram are four-sided figure, hence they are quadrilateral.
Then length of each side of the square are same, hence opposite sides of a square are parallel. The length of opposite side of the parallelogram are parallel to each other. Hence both the square and parallelogram have opposite sides that are parallel.
'All parallelograms are squares?' Do you agree with this statement?
Justify your answer with example/s.
Ans: No I do not agree with this statement. A parallelogram is a quadrilateral with two pairs of parallel sides. Even though the square is like that, there are also other shapes that fulfill these points. A few examples are rhombus, trapezium and rectangle.
Question 5:
ABCD is a parallelogram. If E is midpoint of AD and F is midpoint of BC show, with reasons, that BFDE must be a parallelogram.
Ans: The opposite sides are the same and parallel to each other. The adjacent angles adds up to 180 degrees and the opposite angles are the same.Therefore, we can conclude that it is a parallelogram.
Question 1, 4 , 5 by Kang Yan
Q1.
Based on the above conversation discuss, with examples and justification whether the following statement is justified. 'A square is a rhombus but a rhombus is not a square'. |
A rhombus has 2 pairs of parallel lines and the length of all the sides are equal. A square has 2 pairs of parallel lines, the length of all the sides are equal and has 4 right angles. Since the properties of the square fall under the properties of the rhombus, the square is considered a special type of rhombus.
Source: http://www.analyzemath.com/Geometry/rhombus_problems.html
http://mathforum.org/trscavo/tangrams/area-answers.html
Q4.
'All parallelograms are squares?' Do you agree with this statement?
Justify your answer with example/s.
No, I do not agree with this statement. Just like all surgeons are doctors but not all doctors are surgeons, all squares are parallelograms but not all parallelograms are squares. In order for a parallelogram to be a square as well, it must have 2 pairs of parallel sides, 4 right angles and 4 sides of equal lengths.
Q5.
ABCD is a parallelogram. If E is midpoint of AD and F is midpoint of BC show, with reasons, that BFDE must be a parallelogram.
If BFDE must be a parallelogram, its opposite sides must be of equal length and are parallel to each other. Since E is the midpoint of AD and F is the midpoint of BC, the length of BE should be the same as the length of DF and BE should also be parallel to DF. BF is confirmed parallel to DE. From all these reasons, BFDE must be a parallelogram.
Maths Activity 3 - Michelle Lim.
Question 2, 3 and 4 by Wee Ren Chang
Maths Activity 3-Kristin Chai
The square and parallelogram are quadrilaterals as they are 4 sided which is correct.If the opposite sides of a square and a parallelogram are not parallel,they are not even squares or parallelograms and they will be other shapes.Also,they have a pair of parallel sides if not they will not look like a square or parallelogram.
Q3:It should be a parallelogram as a pair of opposite angles that are supplementary which is 180 degree as the parallelogram have a pair of parallel lines so the angels should be 180 degrees.Even though the other pair of length is not the same,the angels will still add up yo 180 degree.Thus,it is a parallelogram.
Q4: I do not agree with the statement as you see the parallelograms are titled.Even though the lines are parallel the 4 sides of the parallelogram is not the same and also the angels are not 90 degree.So parallelograms are not squares.
Math activity 3 (Q2, 3, 4)
Then length of each side of the square are same, hence opposite sides of a square are parallel. The length of opposite side of the parallelogram are parallel to each other. Hence both the square and parallelogram have opposite sides that are parallel.
Wednesday, August 11, 2010
Thursday, May 27, 2010
Mathematics Essay Writing Competition
Greetings!
Please check out the Main Page of the Google Login for the Essay Competition organised by the Singapore Mathematics Society.
You may participate as an individual or as a team of no more than 3.
As there is a limit to the number of entries to the competition per school, you will have to register through the school.
Saturday, May 8, 2010
Rate Ratio Proportion (What's cooking this week?)
 Cooking for a Party
Cooking for a Party- Click on 'find a recipe' or to Martha Steward Recipe Finder select one recipe that is suitable for the party. You will be cooking a large meal for a party and so will need to change the quantities of the ingredients accordingly. Increase quantities using direct proportion and write a new shopping list.
- All the measurement must be in metric unit (i.e. cm instead of inch)
- The final product:
- An A4 size recipe with cooking direction using Pages.
- include the name and a picture, if possible, of your final dish
- estimated amount of calories
- include a brief writeup why your dish is the best.
- email your 1-page recipe to your Maths teacher with file name classyourname.pages
Friday, May 7, 2010
Rate Ratio Proportion (Resources & Games)
Chap 9: Rate, Ratio and Proportion
- What is/ the key difference/s between ratio and proportion?
- What are the rules you have to observe in ratio and proportion?




SELF DIRECTED LEARNING
- Chapter 9.2: Average Speed
- Chapter 9.3: Speed
Chap 16 Data Handling: Histograms - How does it look like?
- What is a Histogram?
- How different is it from a Bar Chart?


Wednesday, May 5, 2010
STATISTICS (ANALYSIS) : mean, mode & median

- Define the following statistical terms: Mean, Mode and Median
- You may refer to the following link for assistance [click here]

- Provide an example on each of the terms
- When do we use mean, mode or median?
- Use Numbers and Plot a Histogram (label the axes and provide a suitable Title)
- Find the (a) mean, (b) mode and (c) median
- Which of the above averages ie. mean, mode or median you think best represents your findings about your survey? Why?




